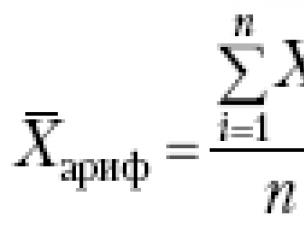ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
«МАТИ» РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. К.Э. ЦИОЛКОВСКОГО
Кафедра «Моделирование систем и информационные технологии»
Числовые ряды
Методические указания к практическим занятиям
по дисциплине «Высшая математика»
Составители : Егорова Ю.Б.
Мамонов И.М.
Корниенко Л.И.
Москва 2005 введение
Методические указания предназначены для студентов дневного и вечернего отделения факультета № 14 специальностей 071000, 130200, 220200.
1. Основные понятия
Пусть
u
1
,
u
2
,
u
3
,
…, u
n
,
…
бесконечная числовая последовательность.
Выражение
 называетсябесконечным
числовым рядом
,
числа u
1
,
u
2
,
u
3
,
…, u
n
членами ряда;
называетсябесконечным
числовым рядом
,
числа u
1
,
u
2
,
u
3
,
…, u
n
членами ряда;
 называется общим членом ряда. Ряд часто
записывают в сокращенном (свернутом)
виде:
называется общим членом ряда. Ряд часто
записывают в сокращенном (свернутом)
виде:
Сумму
первых n
членов числового ряда обозначают через
 и называютn
-й
частичной суммой ряда
:
и называютn
-й
частичной суммой ряда
:
Ряд
называется сходящимся
,
если его n
-я
частичная сумма
 при неограниченном возрастанииn
стремится к конечному пределу, т.е. если
при неограниченном возрастанииn
стремится к конечному пределу, т.е. если
 Число
Число называютсуммой
ряда
.
называютсуммой
ряда
.
Если
же n
-я
частичная сумма ряда при
 не стремится к конечному пределу, то
ряд называютрасходящимся
.
не стремится к конечному пределу, то
ряд называютрасходящимся
.
Пример
1.
Найти сумму
ряда
 .
.
Решение.
Имеем
 . Так как:
. Так как:
 ,
,
Следовательно,

Так
как
 ,
то ряд сходится и его сумма равна
,
то ряд сходится и его сумма равна .
.
2. Основные теоремы о числовых рядах
Теорема
1.
Если
сходится ряд

 то
сходится и ряд
то
сходится и ряд получаемый
из данного ряда отбрасыванием первых
получаемый
из данного ряда отбрасыванием первых членов (этот последний ряд называют
членов (этот последний ряд называют -м
остатком исходного ряда). И наоборот,
из сходимости
-м
остатком исходного ряда). И наоборот,
из сходимости -го
остатка ряда вытекает сходимость данного
ряда.
-го
остатка ряда вытекает сходимость данного
ряда.
Теорема
2.
Если
сходится ряд
 и суммой его является число
и суммой его является число ,
то сходится и ряд
,
то сходится и ряд причем сумма последнего ряда равна
причем сумма последнего ряда равна .
.
Теорема
3.
Если
сходятся ряды

 имеющие соответственно суммыS
и Q,
то сходится и ряд
причем сумма последнего ряда равна
имеющие соответственно суммыS
и Q,
то сходится и ряд
причем сумма последнего ряда равна .
.
Теорема
4
(Необходимый
признак сходимости ряда)
.
Если ряд
 сходится, то
сходится, то ,
т.е. при
,
т.е. при предел общего члена сходящегося ряда
равен нулю.
предел общего члена сходящегося ряда
равен нулю.
Следствие
1.
Если
 ,
то ряд расходится.
,
то ряд расходится.
Следствие
2.
Если
 ,
то определить сходимость или расходимость
ряда с помощью необходимого признака
сходимости нельзя. Ряд может как
сходящимся, так и расходящимся.
,
то определить сходимость или расходимость
ряда с помощью необходимого признака
сходимости нельзя. Ряд может как
сходящимся, так и расходящимся.
Пример 2. Исследовать сходимость ряда:

Решение.
Находим общий член ряда
 .
Так как:
.
Так как:
т.е.
 ,
то ряд расходится (не выполняется
необходимое условие сходимости).
,
то ряд расходится (не выполняется
необходимое условие сходимости).
3. Признаки сходимости рядов с положительными членами
3.1. Признаки сравнения
Признаки сравнения основаны на сравнении сходимости заданного ряда с рядом, сходимость или расходимость которого известна. Для сравнения используются ниже перечисленные ряды.
Ряд
 составленный из членов любой убывающей
геометрической прогрессии, является
сходящимся и имеет сумму
составленный из членов любой убывающей
геометрической прогрессии, является
сходящимся и имеет сумму
Ряд
 составленный из членов возрастающей
геометрической прогрессии, является
расходящимся.
составленный из членов возрастающей
геометрической прогрессии, является
расходящимся.
Ряд
 является расходящимся.
является расходящимся.
Ряд
 называется
рядом Дирихле. При>1
ряд Дирихле сходится, при <1-
расходится.
называется
рядом Дирихле. При>1
ряд Дирихле сходится, при <1-
расходится.
При
=1
ряд
 называется гармоническим. Гармонический
ряд расходится.
называется гармоническим. Гармонический
ряд расходится.
Теорема. Первый признак сравнения. Пусть даны два ряда с положительными членами:
 (2)
(2)
причем
каждый член ряда (1) не превосходит
соответствующего члена ряда (2), т.е.
 (n
=
1, 2, 3, …). Тогда если сходится ряд (2), то
сходится и ряд (1); если расходится ряд
(1), то расходится и ряд (2).
(n
=
1, 2, 3, …). Тогда если сходится ряд (2), то
сходится и ряд (1); если расходится ряд
(1), то расходится и ряд (2).
Замечание.
Этот признак остается в силе, если
неравенствo
 выполняется не при всех
выполняется не при всех ,
а лишь начиная с некоторого номера
,
а лишь начиная с некоторого номера n
=
N
,
т.е. для всех n
N
.
n
=
N
,
т.е. для всех n
N
.
Пример
3.
Исследовать
сходимость ряда

Решение.
Члены данного
ряда меньше соответствующих членов
ряда
 составленного из членов бесконечно
убывающей геометрической прогрессии.
Так как этот ряд сходится, то сходится
и заданный ряд.
составленного из членов бесконечно
убывающей геометрической прогрессии.
Так как этот ряд сходится, то сходится
и заданный ряд.
Теорема.
Второй признак сравнения (предельная
форма признака сравнения).
Если существует конечный и отличный от
нуля предел
 ,
то оба ряда
,
то оба ряда и
и одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
Пример
4.
Исследовать
сходимость ряда

Решение.
Сравним ряд
с гармоническим рядом
 Найдем предел отношения общих членов
рядов:
Найдем предел отношения общих членов
рядов:

Так как гармонический ряд расходится, то расходится и заданный ряд.
Пусть задана последовательность чисел R 1 , R 2 , R 3 ,…,R n ,…. Выражение R 1 + R 2 + R 3 +…+ R n +… называют бесконечным рядом , или просто рядом , а числа R 1 , R 2 , R 3 ,… - членами ряда . При этом имеют в виду, что накопление суммы ряда начинается с первых его членов. Сумма S n = называется частичной суммой ряда : при n=1 – первой частичной суммой, при n=2 – второй частичной суммой и так далее.
Называется ряд сходящимся , если последовательность его частичных сумм имеет предел, и расходящимся – в противном случае. Понятие суммы ряда можно расширить , и тогда некоторые расходящиеся ряды также будут обладать суммами. Именно расширенное понимание суммы ряда будет использовано при разработке алгоритмов при следующей постановке задачи: накопление суммы следует выполнять до тех пор, пока очередной член ряда по абсолютной величине больше заданной величины ε.
В общем случае все или часть членов ряда могут быть заданы выражениями, зависящими от номера члена ряда и переменных. Например,
Тогда возникает вопрос, как минимизировать объём вычислений - вычислять значение очередного члена ряда по общей формуле члена ряда (в приведённом примере её представляет выражение под знаком суммы), по рекуррентной формуле (её вывод представлен ниже) или использовать рекуррентные формулы лишь для частей выражения члена ряда (см. ниже).
Вывод рекуррентной формулы для вычисления члена ряда
Пусть требуется найти ряд чисел R 1 , R 2 , R 3 ,…, последовательно вычисляя их по формулам
 ,
,
 ,
…,
,
…,
Для сокращения вычислений в данном
случае удобно воспользоваться рекуррентной
формулой
вида
 ,
позволяющей вычислить значение R N
при N>1, зная значение предыдущего члена
ряда R N-1 , где
,
позволяющей вычислить значение R N
при N>1, зная значение предыдущего члена
ряда R N-1 , где
 - выражение, которое можно получить
после упрощения отношения выражения в
формуле (3.1) для N к выражению для
N-1:
- выражение, которое можно получить
после упрощения отношения выражения в
формуле (3.1) для N к выражению для
N-1:


Таким
образом, рекуррентная формула примет
вид
 .
.
Из
сравнения общей формулы члена ряда
(3.1) и рекуррентной (3.2) видно, что
рекуррентная формула значительно
упрощает вычисления. Применим ее для
N=2, 3 и 4 зная, что
 :
:

Способы вычисление значения члена ряда
Для вычисления значения члена ряда, в
зависимости от его вида, может оказаться
предпочтительнее использование либо
общей формулы члена ряда, либо рекуррентной
формулы, либо смешанного способа
вычисления значения члена ряда
, когда
для одной или нескольких частей члена
ряда используются рекуррентные формулы,
и затем их значения подставляются в
общую формулу члена ряда. Например,
-
для ряда
проще вычислять значение члена ряда
 по его общей формуле
по его общей формуле
 (сравните с
(сравните с
 - рекуррентной формулой);
- для ряда
- рекуррентной формулой);
- для ряда
 лучше воспользоваться рекуррентной
формулой
лучше воспользоваться рекуррентной
формулой
 ;
- для ряда
следует
применить смешанный способ, вычисляя
A N =X 3N
по рекуррентной формуле
;
- для ряда
следует
применить смешанный способ, вычисляя
A N =X 3N
по рекуррентной формуле
 ,
N=2, 3,… при A 1 =1
и B N =N!
- также по рекуррентной формуле
,
N=2, 3,… при A 1 =1
и B N =N!
- также по рекуррентной формуле
 ,
N=2, 3,… при B 1 =1, а затем – член ряда
,
N=2, 3,… при B 1 =1, а затем – член ряда
 - по общей формуле, которая примет вид
- по общей формуле, которая примет вид
 .
.
Пример 3.2.1 выполнения задания
Вычислить с точностью ε для 0 o X 45 o
используя рекуррентную формулу для вычисления члена ряда:
 ,
,
точное значение функции cos X,
абсолютную и относительную ошибки приближенного значения.
program Project1;
{$APPTYPE CONSOLE}
K=Pi/180; //Коэффициент для перевода из градусов в радианы
Eps: Extended =1E-8;
X: Extended =15;
R, S, Y, D: Extended;
{$IFNDEF DBG} //Операторы, не используемые при отладке
Write("Введите требуемую точность: ");
Write("Введите значение угла в градусах: ");
D:=Sqr(K*X); //Перевод X в радианы и возведение в квадрат
//Задание начальных значений переменным
//Цикл для вычисления членов ряда и накопления их суммы.
//Выполнять, пока модуль очередного члена ряда больше Eps.
while Abs(R)>Eps do
if N<10 then //Вывод, используемый при отладке
WriteLn("N=", N, " R=", R:14:11, " S=", S:14:11);
//Вывод результатов вычислений:
WriteLn(N:14," = Число шагов, за которое достигнута",
"заданная точность");
WriteLn(S:14:11," = Приближенное значение функции");
WriteLn(Cos(K*X):14:11," = Точное значение функции");
WriteLn(Abs(Cos(K*X)-S):14:11," = Абсолютная ошибка");
WriteLn(Abs((Cos(K*X)-S)/Cos(K*X)):14:11,
" = Относительная ошибка");
С помощью данного онлайн калькулятора можно находить суммы рядов, определять их сходимость, абсолютную и условную. Ряд — это последовательность чисел (либо функций — для функциональных рядов), которые связаны между собой определенным законом. Сумма членов ряда это и есть сумма ряда. Для доказательства того, что такая сумма существует (то есть она не равна бесконечности) можно использовать принципы сходимости числовых рядов — принцип Коши, принцип Доламбера и т.д. После доказательства того, что ряд сходится вычислить сумму числового ряда уже необходимо индивидуально. Для геометрической прогрессии, например, сумма вычисляется по формуле:
Найти сумму ряда онлайн
На нашем сайте вы можете вычислить сумму ряда онлайн . Всегда быстро, надежно, бесплатно. Удобный интерфейс для ввода рядов, задание начального и конечного значения элементов. Возможность находить сумму функционального ряда, использование буквенных констант. На практике студенты имеют дело с числовыми рядами довольно часто. Они широко используются в приближенных вычислениях (вычисление интегралов не имеющих аналитического решения, выполнение математических действий, решение дифференциальных уравнений и т.д.). А про функциональные ряды наподобие ряда Тейлора или ряда Фурье и говорить не приходится. С помощью нашего калькулятора определить сумму ряда теперь не проблема.
Определение числовой последовательности
Определения
Численная последовательность
Вызывается серия номеров.

свойство
Код числовой последовательности: (an), (bn), (xn) и т. Д.
(an) = {1, 2, 3, 4, …, n, …} = N. Здесь a1 = 1, a2 = 2, a100 = 100.
(bn) = {-18, 23, 11, -4, 35, …}.
Здесь b1 = -18, b5 = 35.
Серия компьютеров
правила
Окончательная последовательность
— содержит ограниченное количество терминов.
Бесконечная последовательность — Он содержит бесконечное число членов.
Примеры решений
(an) = {1, 5, 8} — конечная последовательность (3 выражения).
(bn) = {10, -10. 10.-10, 10, …} — бесконечная последовательность.
правило
Восходящая последовательность
— a + 1> a для каждого n N, m, e, каждый из следующих членов больше предыдущего.
каждый последующий термин меньше предыдущего.
Примеры решений
1)
-12; 14,5; 18; 40; … является восходящей последовательностью;
2) 4; 2; -1; -7; -11; … последовательность уменьшается;
3) -3; 2; -1; -4; 5; 3; -9 — не растет и не уменьшается;
4) 6; 6; 6; 6; 6; — стационарная (постоянная) последовательность.
правило
! Увеличение и уменьшение строго однообразный
последовательность.
Рассчитать количество онлайн-сериалов
Функция ограничения
Введите функцию и точку, для которой вы хотите вычислить предел
Сайт предлагает подробное решение для поиска ограничений по функциям.
Мы будем вычислять границы функций в точке.
Указанная функция f (x) . Мы вычисляем ваш предел по точке x0
абсолютный (x)
Абсолютное значение х
(модуль х
или | x |
) arccos (x)
Функция — аркоксин из х
arccosh (x)
х
arcsin (x)
Отдельный сын х
arcsinh (x)
HyperX гиперболический х
arctg (x)
Функция — арктангенс из х
arctgh (x)
х
е
е
число — около 2,7 exp (x)
Функция — показатель х
(как е
^х
) log (x)
или ln (x)
Естественный логарифм х
(Да log7 (x)
log10 (x)
= log (x) / log (10)) пи
sin (x)
Функция — Синус х
cos (x)
Функция — Конус от х
sinh (x)
х
cosh (x)
х
sqrt (x)
х
sqr (x)
или x ^ 2
Функция — квадрат х
tg (x)
Функция — Тангенс от х
tgh (x)
х
cbrt (x)
х
почва (х)
Функция округления х
символ (x)
Функция — символ х
erf (x)
Реальные числа введите в форму 7,5 , не 7,5 2 * x — умножение 3 / x — разделение x ^ 3 — eksponentiacija x + 7 — Кроме того, x — 6 — обратный отсчет
Сумма ряда
Введите данные для расчета суммы партии
Найдем сумму многих чисел.
Найдите сумму серии в Интернете
Если это не найдено, система рассчитывает сумму партии с определенной точностью.
Серия сходимости
Этот калькулятор может определить, сходится ли партия, он также показывает, какие критерии сходимости работают, а какие нет.
Он также знает, как определить сходимость степенных рядов.
Она также написала серию, где вы можете увидеть степень сходимости ряда (или расхождения).
Правила ввода терминов и функций
Выражения могут состоять из функций (запись в алфавитном порядке):
абсолютный (x)
Абсолютное значение х
(модуль х
или | x |
) arccos (x)
Функция — аркоксин из х
arccosh (x)
Арксозин является гиперболическим из х
arcsin (x)
Отдельный сын х
arcsinh (x)
HyperX гиперболический х
arctg (x)
Функция — арктангенс из х
arctgh (x)
Арктангенс является гиперболическим х
е
е
число — около 2,7 exp (x)
Функция — показатель х
(как е
^х
) log (x)
или ln (x)
Естественный логарифм х
(Да log7 (x)
, Необходимо ввести log (x) / log (7) (или, например, для log10 (x)
= log (x) / log (10)) пи
Число «Pi», которое составляет около 3,14 sin (x)
Функция — Синус х
cos (x)
Функция — Конус от х
sinh (x)
Функция — Синус гиперболический х
cosh (x)
Функция — косинус-гиперболический х
sqrt (x)
Функция представляет собой квадратный корень из х
sqr (x)
или x ^ 2
Функция — квадрат х
tg (x)
Функция — Тангенс от х
tgh (x)
Функция — касательная гиперболическая от х
cbrt (x)
Функция представляет собой кубический корень х
почва (х)
Функция округления х
на нижней стороне (пример почвы (4.5) == 4.0) символ (x)
Функция — символ х
erf (x)
Функция ошибки (Лаплас или интеграл вероятности)
Следующие операции можно использовать в терминах:
Реальные числа введите в форму 7,5 , не 7,5 2 * x — умножение 3 / x — разделение x ^ 3 — eksponentiacija x + 7 — Кроме того, x — 6 — обратный отсчет
Серия сходимости
Общий член ряда является рациональной частью. Фракцию разлагают на антитело с использованием метода неопределенных коэффициентов:
Выберите счетчик счетчиков счетчика для первой части:
Развернуть скобки:
Теперь мы находим, что находим неизвестные коэффициенты:
После продолжения общий член ряда записывается следующим образом:
Затем мы составим частичную сумму ряда:
Вместе мы получаем:
Для кадров мы страдаем одной секундой:
Заметим, что в скобках есть похожие выражения, которые взаимно уничтожают друг друга. Только два:
Сходимость ряда чисел
Забронированная сумма
Начисленные суммы представляют собой неоплаченные расходы, которые компания включила в отчет о прибылях и убытках.
Обычно это суммы, выплачиваемые через определенные промежутки времени, такие как заработная плата, заработная плата, государственные услуги и вычет подоходного налога с доходов. Например, если баланс находится в середине периода оплаты, платеж в эту дату отображается как сумма, начисленная.
Рассчитанная сумма для отпуска и длинных услуг на счетах потребителей не распространяется, но вычитается полностью на счет созданного резерва.
Предварительно выставленные суммы пенсии, которые пенсионер не требует в установленные сроки, уплачиваются за последние три года до подачи пенсионного требования.
Оплаченная страховая сумма должна распределяться среди сотрудников самозанятых бригад в соответствии с установленной тарифной ставкой и временем работы.
Расчетная сумма выручки облагается НДС.
Предварительно выставленные суммы пенсии, которые не требуются пенсионерам своевременно, выплачиваются в прошлом не более чем за 3 года до подачи пенсионного требования.
Предварительно выставленные суммы пенсии, которые пенсионер не требует в срок, уплачиваются за последние 3 года до подачи требования о выплате пенсии.
Уплаченная пенсия — это сумма, которую пенсионер не выплачивает своевременно, в течение последнего времени, но не более 3 лет (пенсионеры, получающие пенсию в соответствии с Законом о пенсиях и дополнениях для членов колхозов, 15 июля 1964 года — не более 1 года), прежде чем обращаться за пенсией.
Суммы пенсий, которые не были получены в установленный срок по вине органа, назначающего или выплачивающего пенсию, выдается без ограничений в прошлом.
Рассчитанные суммы выплат за отпуск облагаются налогом так же, как и предоплаченные зарплаты.
Начисленные суммы пособий и средств для возмещения дополнительных затрат, которые не были получены процессором своевременно, оплачиваются просроченными, но не более одного года.
Начисленные суммы пособий и средств на возмещение дополнительных расходов, которые они не получили в результате ошибки органа, назначенного и оплаченного ими, выплачиваются на протяжении всего прошедшего периода.
Уплаченная пенсия — это сумма, которую пенсионер не выплачивает своевременно, в течение последнего времени, но не более 3 лет (пенсионеры, получающие пенсию в соответствии с Законом о пенсиях и дополнениях для членов колхозов, 15 июля 1964 года — не более 1 года), прежде чем обращаться за пенсией. Размер пенсии не получает своевременно органом, назначается или выплачивается пенсия, он выдается недавно без каких-либо ограничений.
Платные пенсионные суммы, которые не требуются пенсионерам своевременно, подлежат оплате в течение периода, не превышающего одного года до подачи заявки на получение пенсии.
Поскольку точное значение суммы ряда удается вычислить далеко не всегда (такие задачи были нами рассмотрены), возникает проблема приближенного вычисления суммы ряда с заданной точностью.
Напомним, что
-ый
остаток ряда получается из исходного ряда
получается из исходного ряда отбрасыванием первых
отбрасыванием первых слагаемых:
слагаемых:
Тогда, поскольку для сходящегося ряда
 ,
,
остаток сходящегося ряда равен разности
между суммой ряда и
 -ой
частичной суммой:
-ой
частичной суммой:
 ,
,
и для достаточно больших
 имеем
приближенное равенство
имеем
приближенное равенство
 .
.
Из определения остатка ряда следует,
что абсолютная погрешность при замене
точного неизвестного значения суммы
 его частичной суммой
его частичной суммой равна модулю остатка ряда:
равна модулю остатка ряда:
 .
.
Таким образом, если требуется вычислить
сумму ряда с заданной точностью
 ,
то нужно оставить сумму такого числа
,
то нужно оставить сумму такого числа слагаемых, чтобы для отброшенного
остатка ряда выполнялось неравенство:
слагаемых, чтобы для отброшенного
остатка ряда выполнялось неравенство:
 .
.
Метод приближенного вычисления суммы выбирается в зависимости от вида ряда:
если ряд положительный и может быть исследован на сходимость по интегральному признаку (удовлетворяет условиям соответствующей теоремы), то для оценки суммы используем формулу
 ;
;
если это ряд Лейбница, то применяем оценку:
 .
.
В других задачах можно использовать формулу суммы бесконечно убывающей геометрической прогрессии.
Задача №1.
Сколько нужно взять
слагаемых ряда ,
чтобы получить его сумму с точностью
0,01.
,
чтобы получить его сумму с точностью
0,01.
Решение.
Прежде всего отметим, что
данный ряд сходится. Рассмотрим -ый
остаток ряда, который и является
погрешностью вычислений суммы ряда:
-ый
остаток ряда, который и является
погрешностью вычислений суммы ряда:
Оценим этот ряд с помощью бесконечно
убывающей геометрической прогрессии.
Для этого заменим в каждом слагаемом
множитель
 на
на ,
при этом каждое слагаемое увеличится:
,
при этом каждое слагаемое увеличится:

После вынесения общего множителя за скобку, в скобке остался ряд, составленный из членов бесконечно убывающей геометрической прогрессии, сумму которого мы и вычислили по формуле
 .
.
Заданная точность будет достигнута,
если
 будет удовлетворять условию
будет удовлетворять условию
 .
.
Решим неравенство, учитывая, что
 -
целое.
-
целое.
При
 имеем
имеем
 .
.
При
 имеем
имеем
 .
.
В силу монотонности функции
 ,
неравенство
,
неравенство будет выполняться для всех
будет выполняться для всех .
.
Следовательно, если вместо точного значения суммы мы возьмем первые пять (или более) слагаемых, то погрешность вычислений не превысит 0,01.
Ответ:
 .
.
Задача №2.
Оценить ошибку, получаемую
при замене суммы ряда суммой
первых 100 слагаемых.
суммой
первых 100 слагаемых.
Решение.
Заметим, что данный ряд
является сходящимся и знакопеременным.
Оценивать будем ряд ,
состоящий из модулей исходного ряда,
что сразу увеличивает погрешность
вычислений. Кроме того, нам придется
перейти (используя признак сравнения)
к большему, более простому сходящемуся
ряду:
,
состоящий из модулей исходного ряда,
что сразу увеличивает погрешность
вычислений. Кроме того, нам придется
перейти (используя признак сравнения)
к большему, более простому сходящемуся
ряду:
 .
.
Рассмотрим ряд
 .
Поскольку этот ряд удовлетворяет
условиям теоремы – интегрального
признака сходимости, то для оценки
погрешности вычисления суммы используем
соответствующую формулу:
.
Поскольку этот ряд удовлетворяет
условиям теоремы – интегрального
признака сходимости, то для оценки
погрешности вычисления суммы используем
соответствующую формулу:
 .
.
Вычислим несобственный интеграл:
погрешность вычислений можно оценить по формуле
 ,
,
по условию
 ,
тогда.
,
тогда.
Ответ:
 .
.
Задача №3.
Оценить ошибку,
получаемую при замене суммы ряда суммой
первых 10 слагаемых.
суммой
первых 10 слагаемых.
Решение. Подчеркнем еще раз, что задача о приближенном вычислении суммы имеет смысл только для сходящегося ряда, поэтому, прежде всего отметим, что данный ряд сходится. Поскольку исследуемый ряд является знакопеременным со сложным правилом изменения знака, то оценивать придется, как и в предыдущем примере, ряд из модулей данного ряда:
 .
.
Используя тот факт, что
 при любом значении аргумента, имеем:
при любом значении аргумента, имеем:
 .
.
Оценим остаток ряда:
 .
.
Мы получили ряд, составленный из членов бесконечно убывающей геометрической прогрессии, в которой
 ,
,
его сумма равна:
 ,
,
 .
.
Ответ:
 .
.
Задача №4.
Вычислить сумму ряда с
точностью 0,01.
с
точностью 0,01.
Решение. Данный ряд является рядом Лейбница. Для оценки погрешности верна формула:
 ,
,
другими словами, погрешность вычислений
меньше модуля первого отброшенного
слагаемого. Подберем номер
 так, чтобы
так, чтобы
 .
.
При
 имеем
имеем
 .
.
При
 имеем
имеем
 .
.
Погрешность
 ,
если в качестве значения суммы возьмем
сумму первых четырех слагаемых:
,
если в качестве значения суммы возьмем
сумму первых четырех слагаемых:
Ответ: .
.
Числовой ряд является некой последовательностью, которая рассматривается совместно с другой последовательностью (ее еще называют последовательностью частичных сумм). Подобные понятия применяются в математическом и комплексном анализе.
Сумму числового ряда можно легко вычислить в Excel с помощью функции РЯД.СУММ. Рассмотрим на примере, как работает данная функция, а после построим график функций. Научимся применять числовой ряд на практике при подсчете роста капитала. Но для начала немного теории.
Сумма числового ряда
Числовой ряд можно рассматривать как систему приближений к числам. Для его обозначения применяют формулу:
Здесь показана начальная последовательность чисел ряда и правило суммирования:
- ∑ - математический знак суммы;
- a i - общий аргумент;
- i - переменная, правило для изменения каждого последующего аргумента;
- ∞ - знак бесконечности, «предел», до которого проводится суммирование.
Запись обозначает: суммируются натуральные числа от 1 до «плюс бесконечности». Так как i = 1, то подсчет суммы начинается с единицы. Если бы здесь стояло другое число (например, 2, 3), то суммировать мы начинали бы с него (с 2, 3).
В соответствии с переменной i ряд можно записать развернуто:
А 1 + а 2 + а 3 + а 4 + а 5 + … (до «плюс бесконечности).
Определение суммы числового ряда дается через «частичные суммы». В математике они обозначаются Sn. Распишем наш числовой ряд в виде частичных сумм:
S 2 = а 1 + а 2
S 3 = а 1 + а 2 + а 3
S 4 = а 1 + а 2 + а 3 + а 4
Сумма числового ряда – это предел частичных сумм S n . Если предел конечен, говорят о «сходящемся» ряде. Бесконечен – о «расходящемся».
Сначала найдем сумму числового ряда:

Теперь построим в Excel таблицу значений членов ряда:
Общий первый аргумент берем из формулы: i=3.
Все следующие значения i находим по формуле: =B4+$B$1. Ставим курсор в нижний правый угол ячейки В5 и размножаем формулу.

Найдем значения. Делаем активной ячейку С4 и вводим формулу: =СУММ(2*B4+1). Копируем ячейку С4 на заданный диапазон.


Значение суммы аргументов получаем с помощью функции: =СУММ(C4:C11). Комбинация горячих клавиш ALT+«+» (плюс на клавиатуре).
Функция РЯД.СУММ в Excel
Для нахождения суммы числового ряда в Excel применяется математическая функция РЯД.СУММ. Программой используется следующая формула:

Аргументы функции:
- х – значение переменной;
- n – степень для первого аргумента;
- m – шаг, на который увеличивается степень для каждого последующего члена;
- а – коэффициенты при соответствующих степенях х.
Важные условия для работоспособности функции:
- все аргументы обязательные (то есть все должны быть заполнены);
- все аргументы – ЧИСЛОвые значения;
- вектор коэффициентов имеет фиксированную длину (предел в «бесконечность» не подойдет);
- количество «коэффициентов» = числу аргументов.
Вычисление суммы ряда в Excel
Та же функция РЯД.СУММ работает со степенными рядами (одним из вариантов функциональных рядов). В отличие от числовых, их аргументы являются функциями.
Функциональные ряды часто используются в финансово-экономической сфере. Можно сказать, это их прикладная область.
Например, положили в банк определенную сумму денег (а) на определенный период (n). Имеем ежегодную выплату х процентов. Для расчета наращенной суммы на конец первого периода используется формула:
S 1 = a (1 + x).
На конец второго и последующих периодов – вид выражений следующий:
S 2 = a (1 + x) 2 ; S 3 = a (1 + x) 2 и т.д.
Чтобы найти общую сумму:
S n = a (1 + x) + a (1 + x) 2 + a (1 + x) 3 + … + a (1 + x) n
Частичные суммы в Excel можно найти с помощью функции БС().
Исходные параметры для учебной задачи:

Используя стандартную математическую функцию, найдем накопленную сумму в конце срока сумму. Для этого в ячейке D2 используем формулу: =B2*СТЕПЕНЬ(1+B3;4)

Теперь в ячейке D3 решим эту же задачу с помощью встроенной функции Excel: =БС(B3;B1;;-B2)

Результаты одинаковые, как и должно быть.
Как заполнить аргументы функции БС():

- «Ставка» - процентная ставка, под которую оформлен вклад. Так как в ячейке В3 установлен процентный формат, мы в поле аргумента просто указали ссылку на эту ячейку. Если было бы указано число, то прописывали бы его сотую долю (20/100).
- «Кпер» - число периодов для выплат процентов. В нашем примере – 4 года.
- «Плт» - периодические выплаты. В нашем случае их нет. Поэтому поле аргумента не заполняем.
- «Пс» - «приведенная стоимость», сумма вклада. Так как мы на время расстаемся с этими деньгами, параметр указываем со знаком «-».
Таким образом, функция БС помогла найти нам сумму функционального ряда.
В Excel есть и другие встроенные функции для нахождения разных параметров. Обычно это функции для работы с инвестиционными проектами, ценными бумагами и амортизационными платежами.
Построение графика функций суммы числового ряда
Построим график функций, отражающий рост капитала. Для этого нам нужно построить график функции являющейся суммой построенного ряда. За пример, возьмем те же данные по вкладу:


В первой строке показана накопленная сумма через год. Во второй – через два. И так далее.
Сделаем еще один столбец, в котором отразим прибыль:

Как мы считали – в строке формул.
На основании полученных данных построим график функций.
Выделим 2 диапазона: A5:A9 и C5:C9. Переходим на вкладку «Вставка» - инструмент «Диаграммы». Выбираем первый график:


Сделаем задачу еще более "прикладной". В примере мы использовали сложные проценты. Они начисляются на наращенную в предыдущем периоде сумму.
Возьмем для сравнения простые проценты. Формула простых процентов в Excel: =$B$2*(1+A6*B6)

Добавим полученные значения в график «Рост капитала».

Какие именно выводы сделает инвестор – очевидно.
Математическая формула частичной суммы функционального ряда (с простыми процентами): S n = a (1 + x*n), где а – первоначальная сумма вклада, х – проценты, n – период.